在数据挖掘中有很多地方要计算相似度,比如聚类分析和协同过滤。计算相似度的有许多方法,其中有欧几里德距离、曼哈顿距离、Jaccard系数和皮尔逊相关度等等。我们这里把一些常用的相似度计算方法,用python进行实现以下。如果是初学者,我认为把公式先写下来,然后再写代码去实现比较好。
欧几里德距离
几个数据集之间的相似度一般是基于每对对象间的距离计算。最常用的当然是欧几里德距离,其公式为:

#-*-coding:utf-8 -*-
#计算欧几里德距离:
def euclidean(p,q):
#如果两数据集数目不同,计算两者之间都对应有的数
same = 0
for i in p:
if i in q:
same +=1
#计算欧几里德距离,并将其标准化
e = sum([(p[i] - q[i])**2 for i in range(same)])
return 1/(1+e**.5)
我们用数据集可以去算一下:
p = [1,3,2,3,4,3] q = [1,3,4,3,2,3,4,3] print euclidean(p,q)
得出结果是:0.261203874964
皮尔逊相关度
几个数据集中出现异常值的时候,欧几里德距离就不如皮尔逊相关度‘稳定’,它会在出现偏差时倾向于给出更好的结果。其公式为:
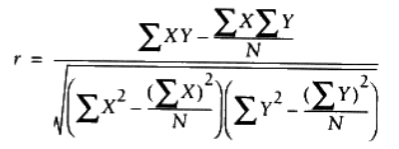
-*-coding:utf-8 -*-
#计算皮尔逊相关度:
def pearson(p,q):
#只计算两者共同有的
same = 0
for i in p:
if i in q:
same +=1
n = same
#分别求p,q的和
sumx = sum([p[i] for i in range(n)])
sumy = sum([q[i] for i in range(n)])
#分别求出p,q的平方和
sumxsq = sum([p[i]**2 for i in range(n)])
sumysq = sum([q[i]**2 for i in range(n)])
#求出p,q的乘积和
sumxy = sum([p[i]*q[i] for i in range(n)])
# print sumxy
#求出pearson相关系数
up = sumxy - sumx*sumy/n
down = ((sumxsq - pow(sumxsq,2)/n)*(sumysq - pow(sumysq,2)/n))**.5
#若down为零则不能计算,return 0
if down == 0 :return 0
r = up/down
return r
用同样的数据集去计算:
p = [1,3,2,3,4,3] q = [1,3,4,3,2,3,4,3] print pearson(p,q)
得出结果是:0.00595238095238
曼哈顿距离
曼哈顿距离是另一种相似度计算方法,不是经常需要,但是我们仍然学会如何用python去实现,其公式为:
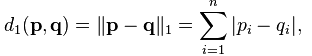
#-*-coding:utf-8 -*-
#计算曼哈顿距离:
def manhattan(p,q):
#只计算两者共同有的
same = 0
for i in p:
if i in q:
same += 1
#计算曼哈顿距离
n = same
vals = range(n)
distance = sum(abs(p[i] - q[i]) for i in vals)
return distance
用以上的数据集去计算:
p = [1,3,2,3,4,3] q = [1,3,4,3,2,3,4,3] print manhattan(p,q)
得出结果为4
Jaccard系数
当数据集为二元变量时,我们只有两种状态:0或者1。这个时候以上的计算相似度的方法就无法派上用场,于是我们引出Jaccard系数,这是一个能够表示两个数据集都是二元变量(也可以多元)的相似度的指标,其公式为:

#-*-coding:utf-8 -*-
# 计算jaccard系数
def jaccard(p,q):
c = [a for i in p if v in b]
return float(len(c))/(len(a)+len(b)-len(b))
#注意:在使用之前必须对两个数据集进行去重
我们用一些特殊的数据集去测试一下:
p = ['shirt','shoes','pants','socks'] q = ['shirt','shoes'] print jaccard(p,q)
得出结果是:0.5
Tanimoto系数
Tanimoto系数是一种度量两个集合之间相似程度的方法(与Jaccard 系数相似,但不是完全相同)。其主要用于二元变量或者多元变量之间的数据集之间的相似度计算,其公式为:
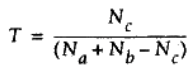
#-*-coding:utf-8-*-
def tanimoto(p,q):
c = [v for v in p if v in q]
return float(len(c) / (len(a) + len(b) - len(c)))
当比较的数据集的数据集合中的元素都是相异的时候,Jaccard系数与Tanimoto系数相同。
# coding: utf-8
#基于分词的文本相似度的计算,
#利用jieba分词进行中文分析
import jieba
import jieba.posseg as pseg
from jieba import analyse
import numpy as np
import os
import pymysql
import threading
connect = pymysql.Connect(
host='localhost',
port=8888,
user='***',
passwd='***',
db='gather',
charset='utf8'
)
cursor = connect.cursor()
mutex = threading.Lock()
'''
文本相似度的计算,基于几种常见的算法的实现
'''
class TextSimilarity(object):
def __init__(file_a,file_b):
'''
初始化类行
'''
str_a = ''
str_b = ''
if not os.path.isfile(file_a):
print(file_a,"is not file")
return
elif not os.path.isfile(file_b):
print(file_b,"is not file")
return
else:
with open(file_a,'r') as f:
for line in f.readlines():
str_a += line.strip()
f.close()
with open(file_b,'r') as f:
for line in f.readlines():
str_b += line.strip()
f.close()
self.str_a = str_a
self.str_b = str_b
#get LCS(longest common subsquence),DP
def lcs(str_a, str_b):
lensum = float(len(str_a) + len(str_b))
#得到一个二维的数组,类似用dp[lena+1][lenb+1],并且初始化为0
lengths = [[0 for j in range(len(str_b)+1)] for i in range(len(str_a)+1)]
#enumerate(a)函数: 得到下标i和a[i]
for i, x in enumerate(str_a):
for j, y in enumerate(str_b):
if x == y:
lengths[i+1][j+1] = lengths[i][j] + 1
else:
lengths[i+1][j+1] = max(lengths[i+1][j], lengths[i][j+1])
#到这里已经得到最长的子序列的长度,下面从这个矩阵中就是得到最长子序列
result = ""
x, y = len(str_a), len(str_b)
while x != 0 and y != 0:
#证明最后一个字符肯定没有用到
if lengths[x][y] == lengths[x-1][y]:
x -= 1
elif lengths[x][y] == lengths[x][y-1]:
y -= 1
else: #用到的从后向前的当前一个字符
assert str_a[x-1] == str_b[y-1] #后面语句为真,类似于if(a[x-1]==b[y-1]),执行后条件下的语句
result = str_a[x-1] + result #注意这一句,这是一个从后向前的过程
x -= 1
y -= 1
#和上面的代码类似
#if str_a[x-1] == str_b[y-1]:
# result = str_a[x-1] + result #注意这一句,这是一个从后向前的过程
# x -= 1
# y -= 1
longestdist = lengths[len(str_a)][len(str_b)]
ratio = longestdist/min(len(str_a),len(str_b))
#return {'longestdistance':longestdist, 'ratio':ratio, 'result':result}
return ratio
def minimumEditDistance(str_a,str_b):
'''
最小编辑距离,只有三种操作方式 替换、插入、删除
'''
lensum = float(len(str_a) + len(str_b))
if len(str_a) > len(str_b): #得到最短长度的字符串
str_a,str_b = str_b,str_a
distances = range(len(str_a) + 1) #设置默认值
for index2,char2 in enumerate(str_b): #str_b > str_a
newDistances = [index2+1] #设置新的距离,用来标记
for index1,char1 in enumerate(str_a):
if char1 == char2: #如果相等,证明在下标index1出不用进行操作变换,最小距离跟前一个保持不变,
newDistances.append(distances[index1])
else: #得到最小的变化数,
newDistances.append(1 + min((distances[index1], #删除
distances[index1+1], #插入
newDistances[-1]))) #变换
distances = newDistances #更新最小编辑距离
mindist = distances[-1]
ratio = (lensum - mindist)/lensum
#return {'distance':mindist, 'ratio':ratio}
return ratio
def levenshteinDistance(str1, str2):
'''
编辑距离——莱文斯坦距离,计算文本的相似度
'''
m = len(str1)
n = len(str2)
lensum = float(m + n)
d = []
for i in range(m+1):
d.append([i])
del d[0][0]
for j in range(n+1):
d[0].append(j)
for j in range(1,n+1):
for i in range(1,m+1):
if str1[i-1] == str2[j-1]:
d[i].insert(j,d[i-1][j-1])
else:
minimum = min(d[i-1][j]+1, d[i][j-1]+1, d[i-1][j-1]+2)
d[i].insert(j, minimum)
ldist = d[-1][-1]
ratio = (lensum - ldist)/lensum
#return {'distance':ldist, 'ratio':ratio}
return ratio
@classmethod
def splitWords(str_a):
'''
接受一个字符串作为参数,返回分词后的结果字符串(空格隔开)和集合类型
'''
wordsa=pseg.cut(str_a)
cuta = ""
seta = set()
for key in wordsa:
#print(key.word,key.flag)
cuta += key.word + " "
seta.add(key.word)
return [cuta, seta]
def JaccardSim(str_a,str_b):
'''
Jaccard相似性系数
计算sa和sb的相似度 len(sa & sb)/ len(sa | sb)
'''
seta = self.splitWords(str_a)[1]
setb = self.splitWords(str_b)[1]
sa_sb = 1.0 * len(seta & setb) / len(seta | setb)
return sa_sb
def countIDF(text,topK):
'''
text:字符串,topK根据TF-IDF得到前topk个关键词的词频,用于计算相似度
return 词频vector
'''
tfidf = analyse.extract_tags
cipin = {} #统计分词后的词频
fenci = jieba.cut(text)
#记录每个词频的频率
for word in fenci:
if word not in cipin.keys():
cipin[word] = 0
cipin[word] += 1
# 基于tfidf算法抽取前10个关键词,包含每个词项的权重
keywords = tfidf(text,topK,withWeight=True)
ans = []
# keywords.count(keyword)得到keyword的词频
# help(tfidf)
# 输出抽取出的关键词
for keyword in keywords:
#print(keyword ," ",cipin[keyword[0]])
ans.append(cipin[keyword[0]]) #得到前topk频繁词项的词频
return ans
@staticmethod
def cos_sim(a,b):
a = np.array(a)
b = np.array(b)
#return {"文本的余弦相似度:":np.sum(a*b) / (np.sqrt(np.sum(a ** 2)) * np.sqrt(np.sum(b ** 2)))}
return np.sum(a*b) / (np.sqrt(np.sum(a ** 2)) * np.sqrt(np.sum(b ** 2)))
@staticmethod
def eucl_sim(a,b):
a = np.array(a)
b = np.array(b)
#print(a,b)
#print(np.sqrt((np.sum(a-b)**2)))
#return {"文本的欧几里德相似度:":1/(1+np.sqrt((np.sum(a-b)**2)))}
return 1/(1+np.sqrt((np.sum(a-b)**2)))
@staticmethod
def pers_sim(a,b):
a = np.array(a)
b = np.array(b)
a = a - np.average(a)
b = b - np.average(b)
#print(a,b)
#return {"文本的皮尔森相似度:":np.sum(a*b) / (np.sqrt(np.sum(a ** 2)) * np.sqrt(np.sum(b ** 2)))}
return np.sum(a*b) / (np.sqrt(np.sum(a ** 2)) * np.sqrt(np.sum(b ** 2)))
def splitWordSimlaryty(self,str_a,str_b,topK = 20,sim =cos_sim):
'''
基于分词求相似度,默认使用cos_sim 余弦相似度,默认使用前20个最频繁词项进行计算
'''
#得到前topK个最频繁词项的字频向量
vec_a = self.countIDF(str_a,topK)
vec_b = self.countIDF(str_b,topK)
return sim(vec_a,vec_b)
@staticmethod
def string_hash(self,source): #局部哈希算法的实现
if source == "":
return 0
else:
#ord()函数 return 字符的Unicode数值
x = ord(source[0]) << 7
m = 1000003 #设置一个大的素数
mask = 2 ** 128 - 1 #key值
for c in source: #对每一个字符基于前面计算hash
x = ((x * m) ^ ord(c)) & mask
x ^= len(source) #
if x == -1: #证明超过精度
x = -2
x = bin(x).replace('0b', '').zfill(64)[-64:]
#print(source,x)
return str(x)
def simhash(self,str_a,str_b):
'''
使用simhash计算相似度
'''
pass
