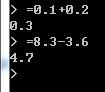
上图是lua的计算结果，可以看到计算结果很准确。下图是python3的计算结果，可以看到计算结果不准确：
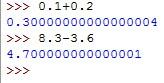javascript中的小数计算也不准确，见这个问题为什么在 javascript 中，小数计算结果常常不准确？山醒在这个问题里给出了答案：因为在计算机中是十进制是以二进制存储的。十进制中的有限不循环小数，在二进制中可能为无限循环小数。比如说：0.3(十进制) = 0.0100110011001100……(二进制)0.6(十进制) = 0.1001100110011001……(二进制)而
计算机精度有限（上面就写了16位），十进制的0.6-0.3在二进制就表现为
0.1001100110011001-0.0100110011001100(二进制)=0.0100110011001101(二进制) =
0.3000030517578125(十进制)好的，误差出来了。
=========问题：lua里边的数字没有整数和小数之分，为什么计算结果十分准确？lua这样做需要额外的代价吗？如果需要，lua为什么要这么做？如果不需要其它脚本语言为什么不这样做（准确计算）？回复内容：
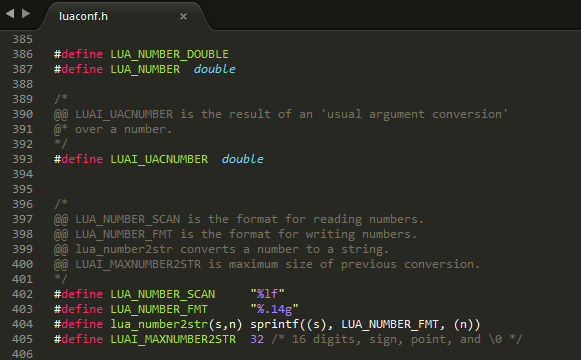
打开 luaconf.h 真相就在眼前。
你的实验并不是因为lua计算的更精确导致的，而是输出这个数字的时候发现小数点后连续一段0就舍弃了后面的内容了…… 比如你可以试试诸如 =1.000000000000001 的结果
说lua小数计算准确的都要去求asin(1)然后print出来
9.4. decimal
decimal numbers can be represented exactly. in contrast, numbers like 1.1 and 2.2 do not have exact representations in binary floating point. end users typically would not expect 1.1 + 2.2 to display as3.3000000000000003 as it does with binary floating point.
在多数语言中，浮点数被设计用做科学计算。想精确地表示一个值？请用int。至于lua，大概是因为不区分整数和浮点类型
显示精度的问题
不支持bignum的语言都是耍流氓。
float 不是这么计算的。 计算机语言带小数点的都是用浮点值储存的。 1个浮点值由三部分构成，正负系数k，指数m和小数点后的底数n 及(-1)的k次幂 乘以 (1.n)的m次幂 得到浮点值。所以才会有你看到的差异。lua为咩显示的只有这么几位，木鸡啦，是不是对算法进行过重构不得而知
學過一小點彙編。計算機在儲存float類型的數據的時候和儲存int類型的數據的方法是不一樣的。先拿int舉一個例子。計算機是以二進制的方法儲存的，那麼舉出任意一個整數，都可以用 符號 ＋ a*2^n+b*2^(n-1)+…x*2^0來表示。 也就是說，理論上來講只要儲存空間足夠大，那麼就可以表示所有的一切的整數。但是float不一樣先說下它的儲存方式吧，其實樓上說的挺對的。float類型數據現在一般有float（單精度浮點數）和double（雙精度浮點數）兩種儲存方式，區別是float用4個byte也就是32個bits而double用64個bits（其實並不知道是不是所有的計算機都這樣，我現在還很小白）每一個bit都可以用0或者1去表示。float是 符號位 ＋ 8bit 指數位 ＋ 23bits 小數位來表示的double是 符號位 ＋ 11bits指數位 ＋ 52bits 小數位來表示的這就出現了 第一個問題， 如果你的數據中小數位超過了 能夠用來表示小數位的bits長度，就會有數據丟失（我指的是能夠被下文的表達方式表示的情況），這種時候計算機通常會按照一定的規則自動round到離原本數據非常近的一個可以表示的數據上（我記得是 round to even？？ 記得不太清楚了） 所以表示的就不準確了。第二個問題，小數的表示方法是1＋a*2^-1 + b*2^-2 + ……. 其結果就是，它會不斷地用一個小的數據去衡量原本數據，但是除了本身就符合這種表達方式的數據之外，其他的數據都無法準確地用這種方式去表達，舉個例子，0.3 樓主可以試試 0.25 ＋ 0.25 和 0.2 ＋ 0.3 當你精度取到一定精確的時候是不一樣的。 這也是為什麼float類型的數一般不用 “＝＝” 去比較而是 去確定一個範圍的原因， 因為有hazard。
这样的事情，要用mathematica来做实验